The goal of this article is to demonstrate the analysis of a market-making strategy’s performance based on market data and trade fills. This is the first of two articles in the series.

Quantitative trading leverages mathematical models and computer science to make data-driven trading decisions. It is widely used by trading firms to provide liquidity, improve market efficiency, and generate profits. But how can one evaluate whether a trading strategy is profitable?

In this article, the objective is to analyse the performance of a market-making strategy on Binance using past ETH/USDC market data. The strategy details are unknown before analysis, with only the data files provided. Python is used for its powerful libraries and suitability for quantitative tasks. A basic grasp of financial mathematics, trading, market dynamics, data analysis, and Python will help in following the analysis presented in this article.

While I cannot share the exact dataset due to its proprietary nature, let’s assume there are two data files available for analysis:

• market_data.parq – Contains market data for ETH/USDC on Binance.
• fills_data.parq – Contains trade fills generated by a market-making strategy on ETH/USDC.

The strategy operates by quoting both bid and ask prices, which aims to provide liquidity while carefully managing positional risk. Because the trading occurs on a spot market, shorting is not an option. Instead, the strategy maintains a target inventory and executes trades to adjust its position accordingly.

In layman’s terms, this strategy works like a store that buys and sells a product at different prices to make a small profit on each trade. It continuously places buy offers at a lower price and sell offers at a higher price, hoping to earn from the price difference. Since it operates in a market where you can only buy and sell what you own (like a regular store, not a betting system), it cannot sell more than it has. Instead, it keeps a certain amount of the product (ETH) in stock and adjusts by buying more when it gets low and selling when it has extra, ensuring it stays balanced while making steady profits.

Note: The nature of quantitative analysis in trading is highly open-ended. While different approaches exist, this analysis is based on one possible method. There is no single “correct” way to analyse a trading strategy, as methodologies can vary based on objectives and data interpretation.

Step 1: Data Loading and Exploration

Jupyter Notebook is used as the coding environment for this analysis.

Import Required Libraries

The necessary libraries are imported to facilitate data manipulation, visualisation, and analysis.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

Load Data from Parquet Files

The Parquet files are loaded into Pandas DataFrames. Ensure that the files market_data.parq and fills_data.parq are located in the correct path.

# Load the Parquet files
market_data = pd.read_parquet("market_data.parq")
fills_data = pd.read_parquet("fills_data.parq")

Inspect Data Information

Since the contents of the Parquet files are not initially known, inspect the data using the info() method for each DataFrame. This provides details about data types, non-null counts, and memory usage.

# Inspect data information
print("Market Data Info:")
print(market_data.info())

print("\nFills Data Info:")
print(fills_data.info())

Output:

Market Data Info:
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 1208954 entries, 2023-06-30 23:45:00.958000+00:00 to 2023-07-15 00:14:59.902000+00:00
Data columns (total 3 columns):
 #   Column   Non-Null Count    Dtype  
---  ------   --------------    -----  
 0   bid_prc  1208954 non-null  float64
 1   ask_prc  1208954 non-null  float64
 2   symbol   1208954 non-null  object 
dtypes: float64(2), object(1)
memory usage: 36.9+ MB
None

Fills Data Info:
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 1123 entries, 2023-07-01 00:46:05.617580 to 2023-07-15 19:04:52.935896
Data columns (total 12 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   order_id          1123 non-null   int64  
 1   side              1123 non-null   object 
 2   fill_prc          1123 non-null   float64
 3   fill_qty          1123 non-null   float64
 4   liquidity         1123 non-null   object 
 5   fee               1123 non-null   float64
 6   fee_ccy           1123 non-null   object 
 7   fee_ccy_usd_rate  1123 non-null   float64
 8   fill_id           1123 non-null   int64  
 9   symbol            1123 non-null   object 
 10  exch              1123 non-null   object 
 11  balance           1123 non-null   float64
dtypes: float64(5), int64(2), object(5)
memory usage: 114.1+ KB
None

The market data consists of 1,208,954 records with three attributes (bid_prc, ask_prc, and symbol), all of which are complete with no missing values. The fills data contains 1,123 records across 12 attributes, capturing trade execution details such as fill_prc, fill_qty, and fee. The significant difference in record count suggests that market data is recorded at a higher frequency compared to fill events.

Inspect Sample Data

To better understand the structure and content of the datasets, the first few rows are displayed using the head() method.

# Inspect sample data
print("Market Data Sample:")
print(market_data.head())

print("\nFills Data Sample:")
print(fills_data.head())

Output:

Market Data Sample:
                                  bid_prc  ask_prc            symbol
timestamp                                                           
2023-06-30 23:45:00.958000+00:00  1934.84  1934.85  binance_eth_usdt
2023-06-30 23:45:01.958000+00:00  1933.77  1933.78  binance_eth_usdt
2023-06-30 23:45:02.958000+00:00  1933.77  1933.78  binance_eth_usdt
2023-06-30 23:45:03.959000+00:00  1933.77  1933.78  binance_eth_usdt
2023-06-30 23:45:04.960000+00:00  1933.77  1933.78  binance_eth_usdt

Fills Data Sample:
                                   order_id side  fill_prc  fill_qty  \  
timestamp                                                              
2023-07-01 00:46:05.617580  670003026938216    S   1937.83    0.0690   
2023-07-01 06:52:59.387733  670003026940777    B   1920.53    0.0264   
2023-07-01 09:19:52.809436  670003026941465    B   1914.23    0.0707   
2023-07-01 10:16:21.048157  670003026941676    B   1916.97    0.1719   
2023-07-01 14:37:25.452850  670003026943147    S   1921.43    0.1719   

                           liquidity       fee fee_ccy  fee_ccy_usd_rate  \  
timestamp                                                                  
2023-07-01 00:46:05.617580     Maker  0.000000     bnb        237.395823   
2023-07-01 06:52:59.387733     Maker  0.000000     bnb        237.395823   
2023-07-01 09:19:52.809436     Maker  0.000000     bnb        237.395823   
2023-07-01 10:16:21.048157     Taker  0.000305     bnb        237.395823   
2023-07-01 14:37:25.452850     Maker  0.000000     bnb        237.395823   

                                        fill_id    symbol     exch  balance  
timestamp                                                                    
2023-07-01 00:46:05.617580  1688172365615000000  eth_usdc  binance   0.3755  
2023-07-01 06:52:59.387733  1688194379383000000  eth_usdc  binance   0.4019  
2023-07-01 09:19:52.809436  1688203192806000000  eth_usdc  binance   0.4726  
2023-07-01 10:16:21.048157  1688206581043000000  eth_usdc  binance   0.6445  
2023-07-01 14:37:25.452850  1688222245450000000  eth_usdc  binance   0.4726  

A review of sample records shows that the market data captures bid and ask prices for the binance_eth_usdt trading pair at high frequency, with price fluctuations occurring at the millisecond level. The fills data provides details on executed orders, including buy (B) and sell (S) transactions, liquidity type (Maker or Taker), and associated fees, with all transactions recorded in the binance_eth_usdc market.

Check for Missing Values

To ensure data completeness, the isnull().sum() method is applied to both datasets to check for any missing values as a precaution.

# Check for missing values
print("Market Data Missing Values:")
print(market_data.isnull().sum())

print("\nFills Data Missing Values:")
print(fills_data.isnull().sum())

Output:

Market Data Missing Values:
bid_prc    0
ask_prc    0
symbol     0
dtype: int64

Fills Data Missing Values:
order_id            0
side                0
fill_prc            0
fill_qty            0
liquidity           0
fee                 0
fee_ccy             0
fee_ccy_usd_rate    0
fill_id             0
symbol              0
exch                0
balance             0
dtype: int64

Both datasets contain no missing values, indicating that the data is complete and ready for analysis. This ensures that further processing can proceed without concerns about data imputation or handling of null values.

Step 2: Data Preparation and Feature Engineering

This step prepares the dataset for analysis by standardising timestamps, merging market data with fills data, and engineering key features such as cash flow and inventory metrics to create a consistent foundation for further insights.

Normalise Timestamps and Sort Data

To ensure consistency, the time zone information is removed from the index of both datasets. Additionally, both datasets are sorted by timestamp to maintain chronological order.

# Remove timezone from market data index for consistency
market_data.index = market_data.index.tz_localize(None)
fills_data.index = fills_data.index.tz_localize(None)

market_data = market_data.sort_index()
fills_data = fills_data.sort_index()

print("Market Data Index:")
print(market_data.index)

print("\nFills Data Index:")
print(fills_data.index)

Output:

Market Data Index:
DatetimeIndex(['2023-06-30 23:45:00.958000', '2023-06-30 23:45:01.958000',
               '2023-06-30 23:45:02.958000', '2023-06-30 23:45:03.959000',
               '2023-06-30 23:45:04.960000', '2023-06-30 23:45:05.960000',
               ...
               '2023-07-15 00:14:59.902000'],
              dtype='datetime64[us]', name='timestamp', length=1208954, freq=None)

Fills Data Index:
DatetimeIndex(['2023-07-01 00:46:05.617580', '2023-07-01 06:52:59.387733',
               '2023-07-01 09:19:52.809436', '2023-07-01 10:16:21.048157',
               '2023-07-01 14:37:25.452850', '2023-07-02 00:15:18.613260',
               ...
               '2023-07-15 19:04:52.935896'],
              dtype='datetime64[us]', name='timestamp', length=1123, freq=None)

The index normalisation ensures that timestamps across both datasets are aligned, preventing potential inconsistencies in time-based operations.

Merge Market Data with Fills Data

To evaluate trade performance in relation to market conditions, the bid and ask prices from the market data are merged with the fills data. This ensures that each trade is matched with the most recent available market price at the time of execution.

A backward search is used, meaning each trade is linked to the latest market price recorded before the transaction.

# Merge the bid and ask prices from market data
fills_data = pd.merge_asof(
    fills_data,
    market_data[['bid_prc', 'ask_prc']],
    left_index=True,
    right_index=True,
    direction='backward'
)

By adding market prices to the fills data, it becomes easier to assess trade execution quality and compare the actual trade price to prevailing market conditions.

Compute Trading Metrics

Calculate Fees in USD

Most exchanges charge trading fees in different currencies. Since this analysis is conducted in USD, fees are converted by multiplying the fee amount by the exchange rate at the time of the trade. This ensures all costs are represented in a consistent currency.

# Compute USD fees
fills_data['fee_usd'] = fills_data['fee'] * fills_data['fee_ccy_usd_rate']

Compute Cash Flow with Fees

Cash flow measures the financial impact of each trade, accounting for trading fees:

• For a sell transaction (S) - Cash flow is the total sale amount minus fees.
• For a buy transaction (B) - Cash flow is the total purchase cost (recorded as a negative value) minus fees.

This calculation helps track how much money is flowing in or out with each trade, providing a clear picture of financial performance.

# Compute cash flow with fees
fills_data['cash_flow'] = np.where(
    fills_data['side'] == 'S',
    fills_data['fill_prc'] * fills_data['fill_qty'] - fills_data['fee_usd'],
    -fills_data['fill_prc'] * fills_data['fill_qty'] - fills_data['fee_usd']
)

Compute Cumulative Cash Balance

To monitor the total cash impact over time, the cumulative sum of cash flow is calculated. This represents the overall financial performance of the trading strategy. Tracking cumulative cash flow helps determine whether the strategy is generating sustainable profits or incurring losses.

# Compute cumulative cash
fills_data['cumulative_cash'] = fills_data['cash_flow'].cumsum()

Compute Inventory Metrics

Calculate Inventory Changes

Each trade affects inventory levels:

• A buy (B) increases inventory, as more assets are acquired.
• A sell (S) decreases inventory, as assets are sold.

Monitoring inventory changes is essential because market-making strategies rely on balancing asset holdings to optimise liquidity provision.

# Compute inventory changes
fills_data['inventory_change'] = np.where(
    fills_data['side'] == 'B',
    fills_data['fill_qty'],
    -fills_data['fill_qty']
)

Compute Cumulative Inventory

The total inventory over time is determined by summing all inventory changes. This cumulative inventory metric helps assess how much of the asset is held at any given time to support risk management and trade planning.

# Compute cumulative inventory
fills_data['cumulative_inventory'] = fills_data['inventory_change'].cumsum()

Step 3: Cash Flow and Inventory Analysis

Understanding how cash flow and inventory levels evolve over time is crucial in evaluating the performance and risk exposure of a market-making strategy. This section visualises these metrics, examines their relationship, and identifies key volatility factors.

Visualise Cumulative Cash and Inventory

A time-series plot is used to visualise cumulative cash flow and cumulative inventory:

• Cumulative cash (blue line) - Tracks the net profit or loss in USD over time.
• Cumulative inventory (red line) - Measures the total amount of assets held at any given moment.

It is easier to see how cash flow is influenced by inventory changes by plotting these metrics together with separate y-axes.

# Visualize cumulative cash and inventory over time
fig, ax1 = plt.subplots(figsize=(16,8))

# Plot cumulative cash on the primary y-axis (left)
ax1.plot(fills_data.index, fills_data['cumulative_cash'], label='Cumulative Cash', color='blue')
ax1.set_xlabel('Timestamp')
ax1.set_ylabel('Cumulative Cash (USD)', color='blue')
ax1.tick_params(axis='y', labelcolor='blue')

# Plot cumulative inventory on a secondary y-axis (right)
ax2 = ax1.twinx()
ax2.plot(fills_data.index, fills_data['cumulative_inventory'], label='Cumulative Inventory', color='red')
ax2.set_ylabel('Cumulative Inventory (Units)', color='red')
ax2.tick_params(axis='y', labelcolor='red')

plt.title("Cumulative Cash and Inventory Over Time")
fig.tight_layout()
plt.show()

Output:

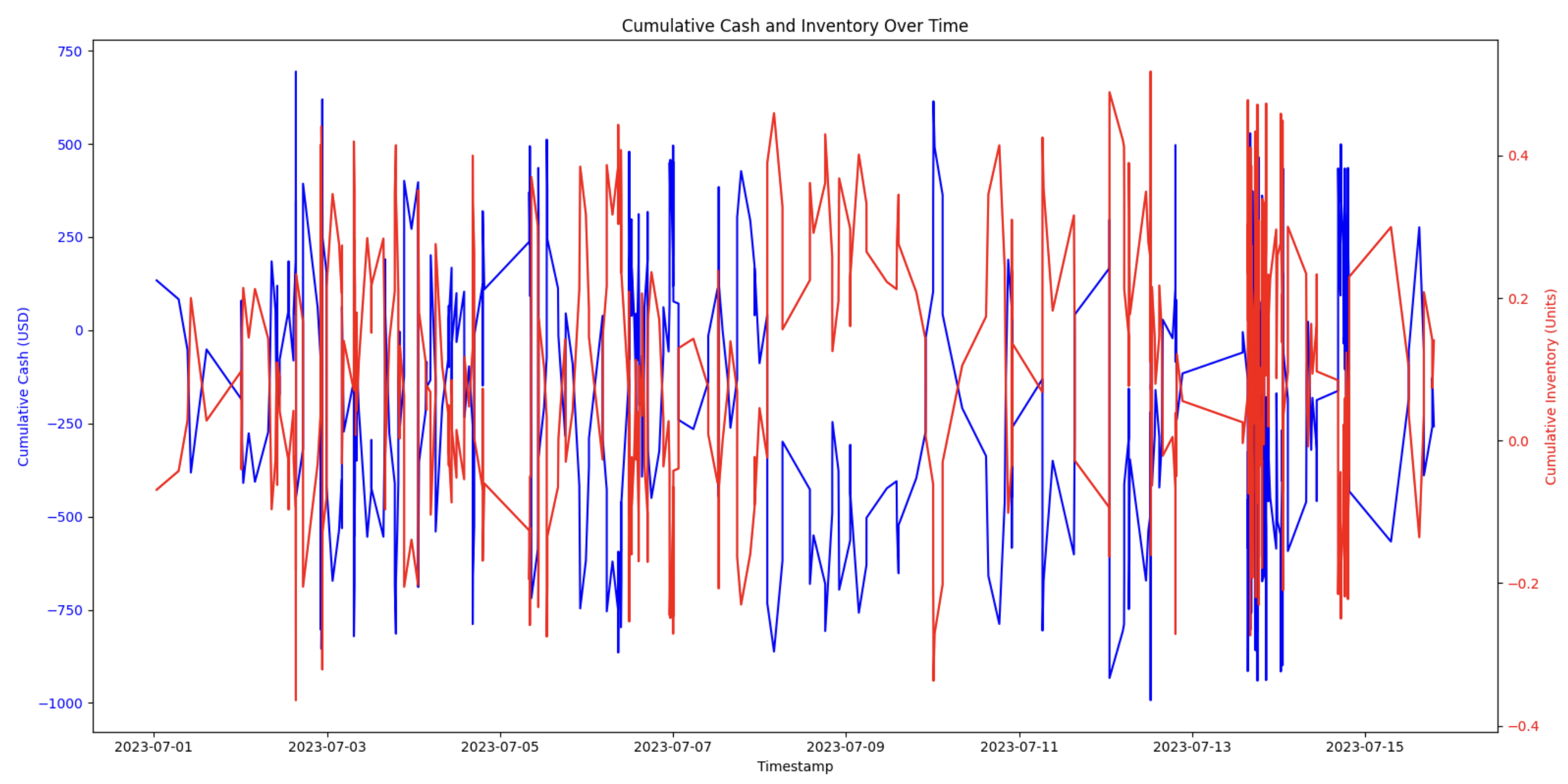
Find the Correlation Between Cash and Inventory

To evaluate the relationship between cash flow and inventory levels, the correlation coefficient is calculated. A value near -1 indicates an expected inverse relationship in market-making, where buying reduces cash and selling increases it. Deviations from this may signal inefficiencies.

• -1 (Perfect Negative Correlation) – Indicates efficient inventory management, where cash decreases with purchases and increases with sales.
• 0 (No Correlation) – Suggests irregular trading behaviour or external influences affecting cash and inventory independently.
• 1 (Perfect Positive Correlation) – Uncommon in market-making, as it suggests both cash and inventory increase together, potentially indicating inefficient inventory management.

# Determine if cash gains/losses are aligned with inventory adjustments
correlation = fills_data['cumulative_cash'].corr(fills_data['cumulative_inventory'])
print("Correlation between Cumulative Cash and Inventory:", correlation)

Output:

Correlation between Cumulative Cash and Inventory: -0.9996847478502905

This near-perfect negative correlation suggests that cash movements are closely tied to inventory adjustments, which aligns with the nature of market-making, where assets are constantly bought and sold while maintaining an inventory balance.

Measure Inventory Volatility

The standard deviation of cumulative inventory is calculated to quantify inventory volatility. A higher standard deviation implies greater fluctuations in inventory levels, indicating more aggressive trading behavior or market instability. This measure helps in assessing how stable the strategy’s inventory management is over time.

# Calculate the standard deviation of cumulative inventory as a measure of volatility
inventory_volatility = fills_data['cumulative_inventory'].std()
print("Inventory Volatility (Std Dev):", inventory_volatility)

Output:

Inventory Volatility (Std Dev): 0.18185536609357372

A moderate level of volatility (Std Dev ≈ 0.18 ETH) suggests the strategy is generally keeping inventory near its target.